没有树链剖分的时代…
没有树链剖分的时代无疑是一个黑暗的时代 —— 明明在线性空间里很简单的问题,在这个扭曲的空间里都变得难以解决。虽然树形结构数据难以计算和统计,但现实生活中又有不少问题和数据需要用树形结构表示和储存。直到有一天,一位天才树学家的出现,为水深火热中的人们带来了希望…
树链剖分的原理
我们仍未知道那位大树学家从何而来,又往何而去,但是他留下的宝贵遗产 —— 树链剖分却彻底颠覆了解决树上问题的方法:将一棵树剖分成多条链,将树上问题转换成了链上问题。形象话地理解,就是把一棵树的枝条砍下来,摆成一行去统计和计算。通过某种规则将树剖分成链,并根据这个规则在访问链式结构的同时又不丢失树形信息,就是树链剖分的目的和核心。
树链剖分的流程
事实上树链剖分的规则不止一种,具体有以子树大小决定优先级的重链剖分,以子树深度决定优先级的长链剖分,以及用于 LCT 的实链剖分。以下只介绍最常用的重链剖分,在不特殊说明的情况下,「树链剖分」即指「重链剖分」。在进行树链剖分之前,我们首先要明确一些变量和概念。对于表示树上一点的 vertex:
father该点在树上的父亲节点depth(有时为distance,有时两者都有)该点的深度subtreeSize以该点为根的子树大小heavySon该点的重多儿子中,子树最大的儿子,称作「重儿子」,重儿子只能有一个 —— 当某点的多个儿子子树大小相同的时候,任选一个作为重儿子即可chainTop该点所在重链的链顶serial[MaxN]每一个 DFN 对应的子节点编号DFN优先遍历重儿子的 DFS 序- 重边和轻边:连接该点与其重儿子的边称为「重边」,剩余的边称为「轻边」。值得注意的是,重边不要求连接的两个节点都是重子节点,而只要求较深的点是较浅的点的重子节点
- 重链:由重边连成的链。特别地,我们将剖分后被孤立的由轻边连成的链也视作重链
树链剖分的核心代码是两次 DFS,上面的图片清晰地展现了一棵树剖分后的样子,我们现在重点来看一下剖分的过程(为了方便起见,请容许我直接使用 DFN 序作为节点的编号)
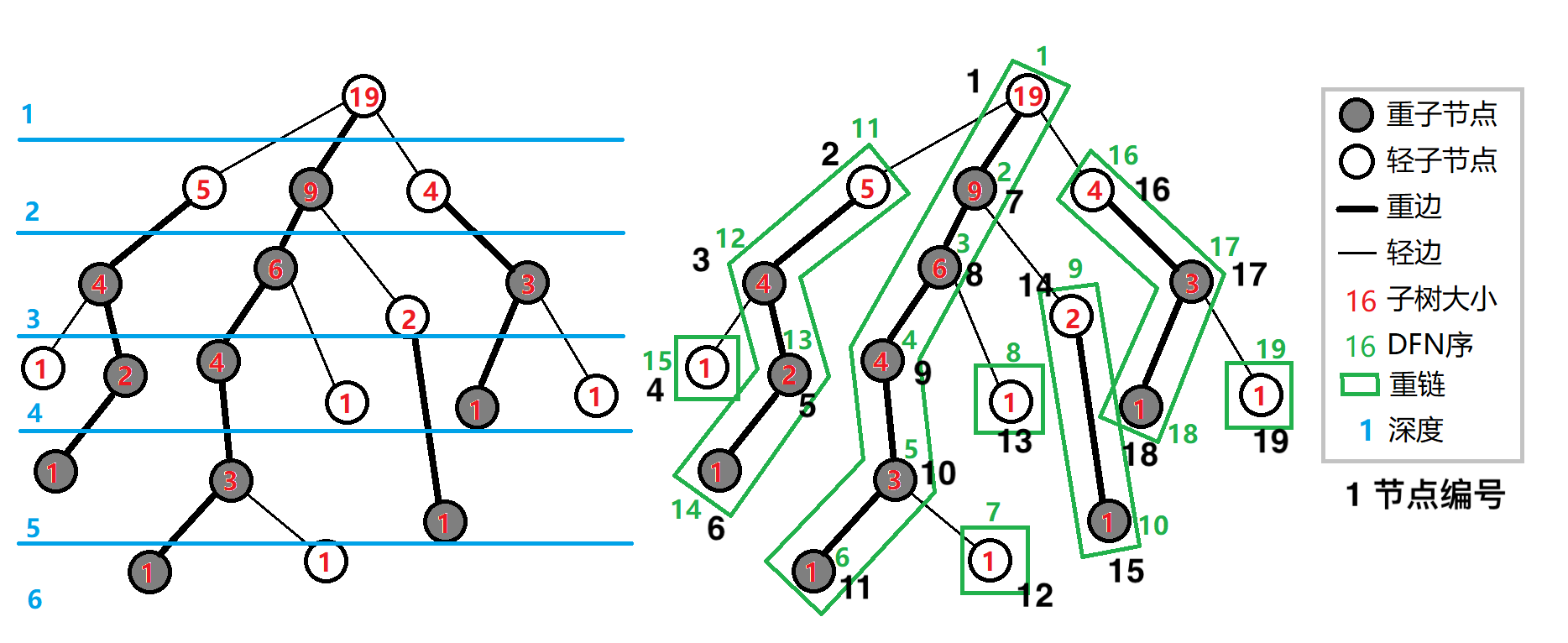
第一次 DFS 处理了节点的深度,父亲,子树大小和重儿子: 从一号点出发,遍历每一个儿子 —— 遍历顺序单纯的依据边添加的顺序,因为这个时候我们还不知道谁是重儿子 —— 在这里我们可以按照从上往下从左往右的顺序。对于每一个儿子,它的深度是父亲深度 +1(离根节点的距离是父亲离根节点的距离加上这条边的权值),父亲是边连接的另一个节点,接着再 DFS 这个子节点,最后将这个儿子的子树大小累加到父亲的子树大小上,并根据儿子的子树大小更新重儿子。例如当我们将 1 号的每一个儿子都便利结束后,可以得到 2 号的子树大小是 5,7 号的子树大小是 9,16 号的子树大小是 4,子树最大的子节点是 7 号,那么 7 号便是 1 号的重儿子。
#define thisSon edge[i].destination
/*The first-time DFS marks each vertex's
father, depth, heavy son, and subtree size*/
inline void DFS1(int x){
vertex[x].subtreeSize = 1;//The father itself contribute to the subtree size
for(int i = head[x]; i; i = edge[i].nextEdge){
if(thisSon == vertex[x].father) continue;//ThisSon shouldn't be the father
vertex[thisSon].depth = vertex[x].depth + 1;
vertex[thisSon].father = x;
DFS1(thisSon);
vertex[x].subtreeSize += vertex[thisSon].subtreeSize;
//Update father's heavy son when the father doesn't have a heavy son or there's a heavier one (with a larger subtree)
if(vertex[thisSon].subtreeSize > vertex[vertex[x].heavySon].subtreeSize) vertex[x].heavySon = thisSon;
}
}
第二次 DFS 处理了节点的 DFN,所在重链的链顶,以及每个 DFN 对应的节点编号:
不妨像添加边一样用一个 cntDFN 记录现在的 DFN 是多少。第二次的 DFS 优先遍历重儿子,当没有重儿子的时候就直接返回。重儿子一定和父亲在同一条重链上,所以对于第二次 DFS 的入口 1 号,其链顶正是它自己,接着优先遍历它的重儿子 7 号,并将 1 号的链顶继承给它。接着再遍历其他的儿子。当然这些儿子和父亲已经不在一条链上,没有继承权的他们只好另起炉灶,以自己作为新的重链的链顶。
#define thisSon edge[i].destination
/*The second-time DFS marks DFN of vertexes,
serial of DFNs, and chain top of the chain that contain certain vertex,*/
inline void DFS2(int x, int top){
vertex[x].DFN = ++cntDFN;
serial[vertex[x].DFN] = x;
vertex[x].chainTop = top;//init: default chainTop is itself
if(!vertex[x].heavySon) return;//to leaf vertex then return
//Mark the heavy son first, because it's on the same chain with the father
//This ensures that the DFN of vertexes on the same chain is continous
DFS2(vertex[x].heavySon, top);
for(int i = head[x]; i; i = edge[i].nextEdge){
//Then mark other sons, but they're not on the same chain with their father
if(thisSon == vertex[x].father || thisSon == vertex[x].heavySon) continue;
DFS2(thisSon, thisSon);
}
}
值得注意的几点:
- 可以发现我们没有对 1 号的深度以及父亲做处理:因为我们将 1 号作为根节点,它是最上级的祖先;在这里我们将根节点的深度定为 0,当然也可以让根节点的深度为 1 —— 事实上图中的树根节点深度就是 1。
- 子树大小的累加应该在对子节点 DFS 之后进行,相当于是向上传递的「归」的过程,DFS 之前子树大小没有被记录,这时候累加只是竹篮打水一场空。
- 因为树链剖分的一般都是无根树,根结点是我们自己定义的,所以在通过边枚举儿子的时候注意跳过父亲。
树链剖分的性质
也许在上面的重链剖分流程中你就已经发现了这些有趣的性质:
- 正如其目的,树链剖分将一棵树完全剖分成若干条重链,每个点必且只属于一条重链 —— 这样才能在将树形结构转化为线性结构时保证节点的不重不漏。
- DFN 是优先遍历重儿子的 DFS 序,所以重儿子的 DFN 和其父亲一定是连续的。所以,由多条重边连成的重链,其上面的节点 DFN 也是连续的。轻儿子紧随重儿子被遍历,所以一颗子树的 DFN 序也是连续的。
- 当向下经过轻边后,子树大小至少减半 —— 某节点拥有轻边仅当它至少拥有至少两个儿子,则一个轻儿子最多分到一半的子树大小。
- 由上一条可得对于树上的任意一条路径,拆成从 LCA 向两边跳链,条链次数为至多 logn 级别。因此任意一条路径中的重链条数都不超过 logn 级别。
树链剖分之后的维护
树链剖分将树上路径转换成线性空间中的一段或多段区间,常使用线段树或树状数组维护。不妨通过P3384 轻重链剖分来熟悉基本应用。
一棵包含 N 个结点的联通且无环的树,每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z
操作2: 格式: 2 x y 表示求树从 x 到 y 结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以 x 为根节点的子树内所有节点值都加上 z
操作4: 格式: 4 x 表示求以 x 为根节点的子树内所有节点值之和

从 x 到 y 的路径由多条重链的片段组成。由于重链中节点的 DFN 是连续的,我们尝试在从 x 跳到 y 的过程中统计 x 走过的重链片段。但是这样做有一个问题:我们记录了每个点的重子节点,它的 DFN 是承接父节点的,但是对于剩下的轻子节点我们并没有严格区分。更何况我们只记录了某点所在重链的链顶,种种因素导致我们只能往上跳而不能往下跳。所以我们可以每次让 x 和 y 链顶深度更深的那一个往上跳链,最终当两个节点在同一条重链上时在深度较浅的节点相会。
在上面的图中,倘若我们要求出 12 号到 15 号的路径,先从 15 号出发,由于 12 号是其所在链的链顶,我们跳到它的父亲 10 号,到达另一条链。这时候 x 的链顶是 1号,深度为1,而 y 的链顶是 14 号,深度为 3 。所以从 15 号出发到其链顶 14 号,由 14 号跳到它的父亲 7 号。这时候两个指针已经处于一条重链,但是没有相会我们让深度较浅的指针找到深度较深的指针,即让处于 10 号的 x 找到处于 7 号的 y。最终我们得出 12 号到 15 号的路径,用 DFN 序表示为 7, 5-2, 9-10,但是程序运势运行时累加答案的顺序是 7, 9-10, 2-5。
可以两个指针最终总是在 LCA 处相会,也许你已经意识到了出现这种情况的原因:由于只能向上跳链,所以我们在跳链之初就是将从 x 到 y 的路径拆成了从 LCA 向下走的两条路。事实上在利用树链剖分解决两点之间路径上的问题时,我们总能顺便求出他们的 LCA。
在完整子树上的操作和询问就简单很多:以 x 为根的子树,其 DFN 序是连续的,是从 vertex[x].DFN 到 vertex[x].DFN + vertex[x].subtreeSize - 1。这里减去 1 是为了去除重复统计的根节点 x。
为上面的例题献上代码:
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#define thisSon edge[i].destiVertex
#define xTop vertex[x].chainTop
#define yTop vertex[y].chainTop
using namespace std;
const int MaxN = 1000005;
int n, m, root, mod, finalValue[MaxN];
struct Vertex{
int val, father, depth, subtreeSize, heavySon, chainTop, DFN;
//Differ from finalValue, vertex[x].val record the input vertex value, which had not been re-numbered yet
}vertex[MaxN];
struct Edge{
int destiVertex, nextEdge;
}edge[MaxN * 2];
struct SegmentTree{
int data, addTag, l, r;
}seg[MaxN * 4];
int tot, head[MaxN], cntDFN;
inline void AddEdge(int u,int v){
edge[++tot].destiVertex = v;
edge[tot].nextEdge = head[u];
head[u] = tot;
}
/*The first-time DFS marks each vertex's
father, depth, heavy son, and subtree size*/
inline void DFS1(int x){
vertex[x].subtreeSize = 1;//The father itself contribute to the subtree size
for(int i = head[x]; i; i = edge[i].nextEdge){
if(thisSon == vertex[x].father) continue;//ThisSon shouldn't be the father
vertex[thisSon].depth = vertex[x].depth + 1;
vertex[thisSon].father = x;
DFS1(thisSon);
vertex[x].subtreeSize += vertex[thisSon].subtreeSize;
//Update father's heavy son when the father doesn't have a heavy son or there's a heavier one (with a larger subtree)
if(vertex[thisSon].subtreeSize > vertex[vertex[x].heavySon].subtreeSize) vertex[x].heavySon = thisSon;
}
}
/*The second-time DFS marks DFN of vertexes,
Rank of DFNs, and chain top of the chain that contain certain vertex,*/
inline void DFS2(int x, int top){
vertex[x].DFN = ++cntDFN;
finalValue[vertex[x].DFN] = vertex[x].val;
vertex[x].chainTop = top;//init: default chainTop is itself
if(!vertex[x].heavySon) return;//to leaf vertex then return
//Mark the heavy son first, because it's on the same chain with the father
//This ensures that the DFN of vertexes on the same chain is continous
DFS2(vertex[x].heavySon, top);
for(int i = head[x]; i; i = edge[i].nextEdge){
//Then mark other sons, but they're not on the same chain with their father
if(thisSon == vertex[x].father || thisSon == vertex[x].heavySon) continue;
DFS2(thisSon, thisSon);
}
}
//SegmentTree below
//Because of the contiguity of vertex DFNs, we can use segment tree as the statistic of range answer
inline void PassTag(int x){
seg[x*2].data = (seg[x*2].data + (seg[x*2].r - seg[x*2].l+1) * seg[x].addTag) % mod;
seg[x*2+1].data = (seg[x*2+1].data + (seg[x*2+1].r - seg[x*2+1].l+1) * seg[x].addTag) % mod;
seg[x*2].addTag = (seg[x*2].addTag + seg[x].addTag) % mod;
seg[x*2+1].addTag = (seg[x*2+1].addTag + seg[x].addTag) % mod;
seg[x].addTag = 0;
}
inline void Build(int x,int l,int r){
seg[x].l = l, seg[x].r = r;
if(seg[x].l == seg[x].r){
seg[x].data = finalValue[l];
return;
}
int mid = (l + r) / 2;
Build(x*2, l, mid);
Build(x*2+1, mid+1, r);
seg[x].data = (seg[x*2].data + seg[x*2+1].data) % mod;
}
//Ask and Addition are two basic segment-tree functions used in other higher-level function
inline void Addition(int x,int l,int r,int z){
if(seg[x].l >= l && seg[x].r <= r){
seg[x].data = (seg[x].data + (seg[x].r - seg[x].l + 1) * z) % mod;
seg[x].addTag = (seg[x].addTag + z) % mod;
return;
}
if(seg[x].addTag) PassTag(x);
int mid=(seg[x].l+seg[x].r)/2;
if(l <= mid) Addition(x*2, l, r, z);
if(r > mid) Addition(x*2+1, l, r, z);
seg[x].data = (seg[x*2].data + seg[x*2+1].data) % mod;
}
inline int Ask(int x,int l,int r){
int ans = 0;
if(seg[x].l >= l && seg[x].r <= r) return seg[x].data;
if(seg[x].addTag) PassTag(x);
int mid = (seg[x].l + seg[x].r) / 2;
//Remember to mod here, or ans will overflow
if(l <= mid) ans = (ans + Ask(x*2, l, r)) % mod;
if(r > mid) ans = (ans + Ask(x*2+1, l, r)) % mod;
return ans % mod;
}
//SegmentTree above
//Problem tasks below
//Just move x to the chain that y is on, add answer on the way, and then add range answer from x to y
inline void WayAdd(int x,int y,int z){
//Keep x moving until x and y are on the same chain
while(xTop != yTop){
if(vertex[xTop].depth < vertex[yTop].depth) swap(x,y);
Addition(1, vertex[xTop].DFN, vertex[x].DFN, z);
//jump from one chain to another
x=vertex[xTop].father;
}
if(vertex[x].depth > vertex[y].depth) swap(x,y);
Addition(1, vertex[x].DFN, vertex[y].DFN, z);
}
inline int WayAsk(int x,int y){
int ans=0;
//same as WayAdd
while(xTop != yTop){
if(vertex[xTop].depth < vertex[yTop].depth) swap(x,y);
ans=(ans + Ask(1, vertex[xTop].DFN, vertex[x].DFN)) % mod;
x=vertex[xTop].father;
}
if(vertex[x].depth > vertex[y].depth) swap(x,y);
ans = (ans + Ask(1, vertex[x].DFN, vertex[y].DFN)) % mod;
return ans;
}
inline void SubtreeAdd(int x, int z){
Addition(1, vertex[x].DFN ,vertex[x].DFN + vertex[x].subtreeSize - 1, z % mod);
}
inline int SubtreeAsk(int x){
return Ask(1, vertex[x].DFN ,vertex[x].DFN + vertex[x].subtreeSize - 1);
}
//Problem tasks above
int main(){
scanf("%d%d%d%d",&n,&m,&root,&mod);
for(int i = 1; i <= n; i++) scanf("%d",&vertex[i].val);
for(int i = 1; i < n; i++){
int u, v;
scanf("%d%d",&u,&v);
AddEdge(u, v);
AddEdge(v, u);
}
DFS1(root);
DFS2(root,root);
Build(1,1,n);
while(m--){
int op, x, y, z;
scanf("%d",&op);
if(op==1){
scanf("%d%d%d",&x,&y,&z);
WayAdd(x,y,z%mod);
}
if(op==2){
scanf("%d%d",&x,&y);
printf("%d\n",WayAsk(x,y));
}
if(op==3){
scanf("%d%d",&x,&z);
SubtreeAdd(x, z);
}
if(op==4){
scanf("%d",&x);
printf("%d\n",SubtreeAsk(x));
}
}
return 0;
}
这段代码只是为了让大家感受一下树链剖分在完整的题中和数据结构结合的写法。在打板子的时候一定要自己调代码直到 AC 哦 —— 这样才能真正理解树剖的实现。其实只是因为我调这个板子调了两天 QwQ。下面我们来看几道题吧。
P2146 软件包管理器
软件包的依赖关系形成一个树形结构,除了不依赖任何软件包的 0 号软件包,每个软件包只直接依赖一个软件包,一开始所有的软件包都未安装。现在有两种操作:
install x要求安装 x 号软件包,想要安装软件包 x 必须安装它依赖的软件包uninstall x要求卸载 x 号软件包,想要卸载 x 号软件包必须先卸载直接或间接依赖它的软件包。 对于每次操作,你需要计算出这次操作会改变多少软件包的安装状态,并应用这个操作。
我们用每个点的权值表示它的安装状态(1 和 0),那么安装软件包 x 就是将 x 到根节点路径上的点权值都变为 1,卸载软件包 x 就是将以 x 为根的子树上的点的权值都变为 0。显然可以先树剖进行处理。
考虑如何统计被改变状态的点的数量:我们可以用操作前后状态和的差值表示。每次操作前询问操作空间的状态和 sum1,操作后操作空间的状态和 sum2,安装就是 sum2-sum1,卸载就是sum1-sum2。
P3313 旅行
一个宗教信仰自由的国家有 n 个城市,呈树形结构,每个城市的居民只信仰一种宗教,且有一个旅行评级。该国居民爱好旅行,但是为了避免与信仰不同的异邦人发生冲突,他们只去相同信仰的城市,且只在相同信仰的城市停留。现有以下四种事件:
- 城市 x 全体居民改信 c 教
- 城市 x 旅行评级调整为 w
- 某旅行者从 x 出发到 y,记下中途停留的城市的评级总和
- 某旅行者从 x 出发到 y,记下中途停留的城市的评级最大值
如果没有宗教的限制,本题就是一道简单的树剖+线段树题,所以限制宗教信仰有利于统治者的管理,我们现在考虑如何处理宗教信仰。
信仰 c 教的旅行者只去信仰 c 教的城市,且只在信仰 c 教的城市停留,也就是说途中的异教城市与他无关。这样一来我们可以对这些城市视而不见,仅把路程累加到同教城市之间。我们可以给每一种宗教开一颗线段树,到时候只需要在相应的线段树上进行修改和查询即可。值得注意的是本题数据范围中 $C≤10^{5}$,所以直接开线段树就只能等着 MLE,使用动态开点线段树可以避免暴毙。动态开点线段树与传统的线段树很相似,只是舍弃了使用数组下标表示左右儿子的方式而是把儿子的序号单独记录下来 —— 如果你使用线段树的结构体写法可以很方便的转换过来。记得在动态开点修改时要使用取地址符,因为此时你不知道要修改的位置是否开了点。
P4211 LCA
给出一棵树,并有若干次询问,每次询问给出 l, r, z, 求 $\large\Sigma^{r}_{i=l}dep[LCA(i,z)]$
我们可以暴力求 LCA 然后把深度加起来,但是显然是过不了的 —— 我们要考虑如何将这么一坨转化成好求的东西。
在学习 LCA 之初,我们就知道两个点的 LCA (x, y) 的深度就是 x y 到根的公共路径长度。那么将边的默认权值设为0,把 x 到根的路径上所有的边权赋为 1,再统计 y 到根的路径长度,这个值就是 LCA 的深度。因为 y 到根的路径显然可以拆成 y 到 LCA (x, y) 和 LCA (x, y) 到根两部分。其中 LCA (x, y) 到根的这一段被标记过了,而我们要求的 LCA 深度就是这一段。这道题中每次询问的终点 z 是不变的,起点是一个区间,我们可以根据差分思想将题目中的 $[l,r]$ 转化为$[1,r]-[1,l-1]$。
现在我们尝试求每次询问中 $[1,x]$ 到 $v$ 对答案的贡献,显然可以对于每次询问把 $[1,x]$ 到根节点的路径上边权 +1,然后统计 v 到根节点的路径长度。但是这样就会进行很多重复的标记,即使我们可以通过每次询问后清除标记防止答案重复累加,我们还是不断地添加并清除同一个位置的标记,时间复杂度会很大。
而 $[1,x]$ 与 $[1,x+1]$ 显然有很多很多公共部分,于是我们可以将询问离线,差分处理后按照 x 从小到大排序,对于每一个 x 处理含有它的询问的每一个 v,将答案累加到一个ans[]数组中。处理结束后在原有的基础上对 x+1 到根的路径打标记,再用相同方法处理 x+1,以此类推。
P4556 雨天的尾巴
n 座房屋构成一个树形结构。救济粮发放 m 次,每次给从 x 到 y 路径上的房子发放一袋 z 类型的救济粮,求发放终了后每座房子中那种救济粮最多。
这道题是洛谷上线段树合并的模版,不过可以使用常数更小的树剖+线段树解法。用树剖将路径修改转换成若干个区间修改,然后根据差分思想,将区间 $[x,y]$ 增加 z 的修改变为在 x 处打一个正标记在 y 处打一个负标记的单点修改,用线段树维护即可。
大体思路很容易,可是我们怎样区分不同种类的救济粮呢?在线段树合并做法中,我们正是为了区分不同种类的救济粮而给每个点开了一棵权值线段树,而在树剖做法中我们可以给每一个节点开一个 vector 来储存救济粮的种类和对应的标记:
struct Vertex{
int father, depth, DFN, subtreeSize, chainTop, heavySon;
vector< pair<int,int> > item;
}vertex[MaxN];
inline void TreeAdd(int x,int y,int z){
while(xTop!=yTop){
if(vertex[xTop].depth < vertex[yTop].depth) swap(x,y);
vertex[vertex[xTop].DFN].item.push_back(make_pair(z,1));
vertex[vertex[x].DFN+1].item.push_back(make_pair(z,-1));
x = vertex[xTop].father;
}
if(vertex[x].depth > vertex[y].depth) swap(x,y);
vertex[vertex[x].DFN].item.push_back(make_pair(z,1));
vertex[vertex[y].DFN+1].item.push_back(make_pair(z,-1));
}
vector 中再放种类和标记的二元组,就可以轻松统计每个点不同种类救济粮的信息啦!
P1600 天天爱跑步
n 个节点的树上有 m 个人,每个人都想好了起点 S 和终点 T。所有人都同时从自己心的起点出发,跑向心目中的终点,速度是 $1edge/s$。每个点上有一个观察员,每个观察员都选择一个时间 W 观察玩家,一个玩家可以被某个点的观察员观察到当且仅当他在这个点观察员观察的时间恰好到达这个点。求每个点的观察员各能够观察到几个人。
对于第 i 个人,他的跑步路径可以分成两段:从 $S_{i}$ 到 $LCA(S_{i},T_{i})$ 以及从 $LCA(S_{i},T_{i})$ 到 $T_{i}$。值得注意的是,LCA 只包含在其中的一段中。对于节点 x 的观察员,他能观察到第 i 个人有两种情况:
- 节点 x 在第一段路上,这时需要满足 $depth[S_{i}]-depth =w $
- 节点 x 在第二段路上,这时需要满足 $depth[S_{i}]+depth -2*depth[LCA(S_{i},T_{i})]=w $
由于具有两种不同的规则,我们将一个点的观察员在两种规则下观察到的玩家分别计算最后再加起来。乍看仿佛无法下手,但是将上面的两个式子移一下项就可以变成 $depth[S_{i}]=w[x]+depth[x]$ 和 $depth[S_{i}]-2depth[LCA(S_{i},T_{i})]=w[x]-depth[x]$。结合上一道题,本题可以转换成「第 i 次操作给 $S_{i}$ 到 $LCA(S_{i},T_{i})$ 上的每一个房屋发放一袋类型为 $depth[S_{i}]$ 的救济粮,并给 $LCA(S_{i},T_{i})$ 到 $T_{i}$ 的每一个房屋发放一袋类型为 $depth[S_{i}]-2depth[LCA(S_{i},T_{i})]$ 的救济粮,最终求每个节点处 $w[x]+depth[x]$ 和 $w[x]-depth[x]$ 类型的救济粮共多少袋」。做法也是相似的 —— 对每一个点开一个 vector,利用差分统计。不过和上一题有所不同的是,本题要求的是和而不是数量最多的类型,所以可以直接用前缀和统计而不需要另写一个统计函数寻找最大值。
树链剖分求 LCA 的综合应用
树链剖分所解决的问题基本都与 LCA 相关,在一些综合题中常有 LCA 的应用,这时使用树链剖分不仅可以方便地求 LCA,还可以简化后续问题,帮助我们求解。
AcWing355 异象石
有N个点,有N-1条双向边把它们连通起来。起初地图上没有任何异象石,在接下来的M个时刻中,每个时刻会发生以下三种类型的事件之一:
地图的某个点上出现了异象石(已经出现的不会再次出现)
地图某个点上的异象石被摧毁(不会摧毁没有异象石的点)
询问使所有异象石所在的点连通的边集的总长度最小是多少
LYD 蓝书上写道「仔细思考可以发现,如果我们按照 DFN 从大到小排序,把出现异象石的节点排成一圈(首尾相接),并且累加相邻两个节点之间的路径长度,最后得到的结果恰好是所求答案的两倍」这可能让人有点摸不着头脑,我们现在来「仔细思考」一下。
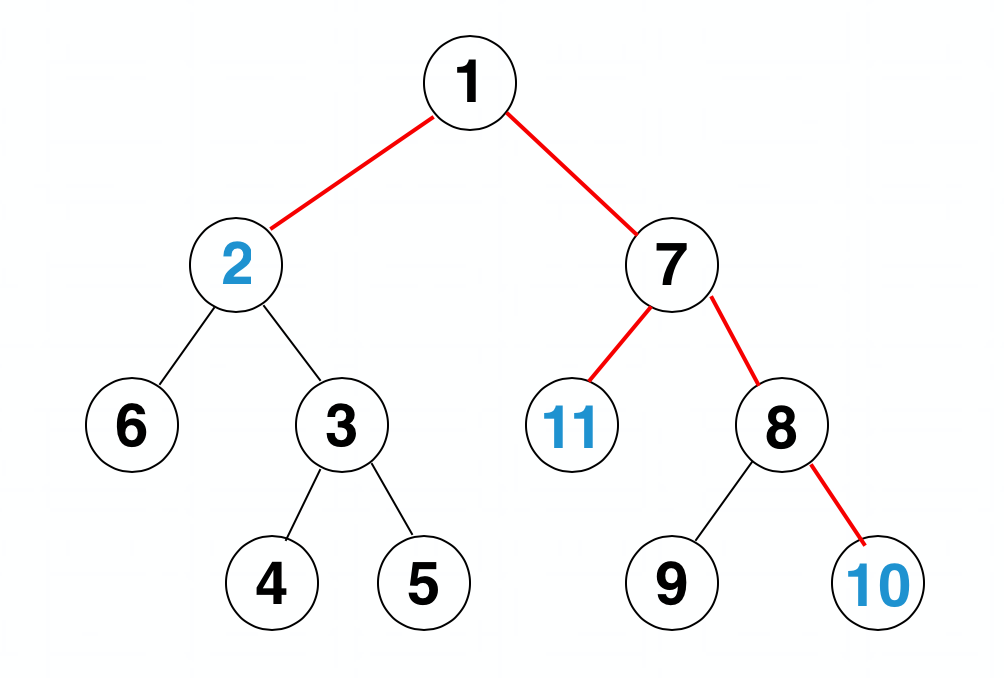
在这幅图中,我们用 DFN 作为节点的标号,2,10,11 号是异象石,红色的边权总和便是我们要求的答案。从所有异象石的 LCA 出发,以类似 DFS 的方式找所有的异象石,每条红边都被走过两次。所有异象石的 LCA 可以通过求 LCA 的 LCA 得到:$LCA(11,10)=7,LCA(2,11)=1,LCA(2,10)=1,LCA(1,7)=1,LCA(1,1)=1$。而且每两个异象石之间的路径都可以拆成从它们的 LCA 向下走的两段 —— 一个是先求总的 LCA 再求总的路径,一个是两两求 LCA,然后一段一段走,最终每条边都走了两次。所以我们假设现在有异象石集合 {s},那么我们要求的答案就可以表示为 $answer=(dis(s_{i},s_{i+1})+dis(s_{i+1},s_{i+2})+…+dis(s_{n-1},s_{n})+dis(s_{n},s_{1}))/2$。不要忘记最后的一项。
想到这里,剩下就基本是常规的树剖 LCA 应用了。用 set 维护异象石节点序列,并用一个变量 ans 动态记录异象石出现的不同状态下红边边权之和。对于两点 x y 有 $dis(x,y)=depth[x]+depth[y]-2*depth[LCA(x,y)]$。当某一节点 x 出现异象石,就把它放入集合,若它的前后节点为 a b,有 ans+=dis(a,x)+dis(x,b)-dis(a,b)。某点异象石消失就减去。
顺便提供一个双倍经验,稍有区别但基本一样: P3320 寻宝游戏
树链剖分的非传统应用
LOJ6669 奈绪和二叉树
一道交互题。有 n 个节点(n ≤ 3000),以 1 号点为根的二叉树,你可以询问树上两点间的距离,但是询问次数不能超过 30000 次。你需要求出每个节点的父亲。
通过上面的题目,一个思想已经在我们的脑中根深蒂固:我们可以用点的深度计算点的距离。而在本题中我们可以询问两点之间的距离 —— 那么我们是不是可以通过将其与点的深度联系在一起,来推出树上的其他信息呢?
首先很容易想到,一个节点的深度就是它与根节点的距离 —— 我们知道根节点是 1 号节点,那么就可以通过 n - 1 次询问求出每个点的深度。因为要求出每个节点的父亲,所以我们一层一层往下扩展,这样找到新节点的时候它的父亲就已经知道了,可以由已知求解未知。
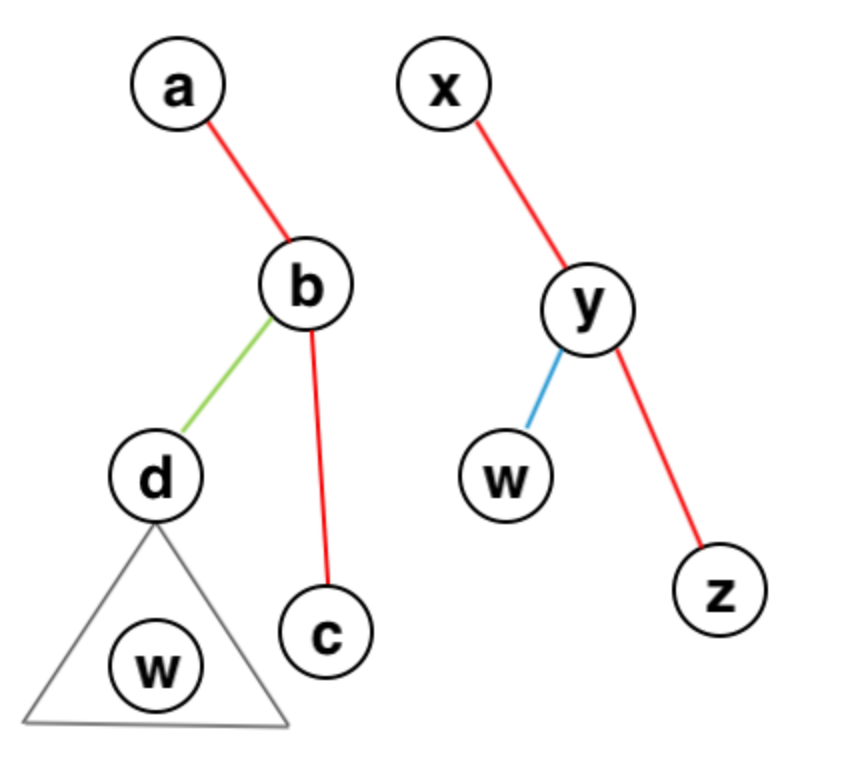
在寻找一个点之前我们先对已知的树进行剖分,红边代表重链,x y z 和 a b c 都是重链上的点。我们想要寻找 w 的父亲,于是询问 w 与当前已知重链底端的距离,这样就可以求出他们 LCA 的深度。如果这个深度比 w 的深度小 1,那么 LCA 就是 w 的父亲,如右图 y 就是 w 的父亲。而如果深度相差大于 1,那么我们求走到 LCA 的轻儿子,再它的子树中重复刚才的过程。由于这是一颗二叉树, 亲轻儿子是唯一的。