关于树的直径
连接树上相距最远的两点的路径被称作这棵树的最长链。树的直径指这条最长链或者它的长度。
树的直径的求法
一般来将我们可以使用两种方法求数的直径，它们的时间复杂度都是 $O(n)$。
两次搜索
我们可以通过两次 DFS 或两次 BFS 来求树的直径，其原理非常简单：从任意一个节点 $start$ 出发进行第一次搜索，找到距离起点最远的点（记为 $deepest$），再从 $deepest$ 出发进行第二次搜索，找到距离它最远的点（记为 $ending$）。$deepest$ 和 $ending$ 之间的路径便是这棵树的直径，在这个过程中 $deepest$ 一定是直径的一端，否则第一次搜索的结果一定不是 $deepest$，因为直径的两个端点中一定有一个比 $deepest$ 离 $start$ 远。
#define des edge[i].destinationVertex
inline void BFS(int x, int secondTime){
Reset();
queue<int> q;
q.push(x);
vertex[x].vis = true;
while(!q.empty()){
int cur = q.front();
q.pop();
for(int i=head[cur];i;i=edge[i].nextEdge){
if(!vertex[des].vis){
vertex[des].vis = true;
vertex[des].depth = vertex[cur].depth + edge[i].value;
q.push(des);
if(secondTime) vertex[des].father = cur;
}
}
}
for(int i=1;i<=n;i++)
if(treeLength < vertex[i].depth){
treeLength = vertex[i].depth;
deepest = i;
}
}
不同于接下来只能统计直径长度的树形 DP，在第二次搜索中，我们可以记录每一个点第一次被访问时的父亲节点，最后从搜索到的 $ending$ 往回走，就可以取得这条直径。两次搜索的方法虽然码量稍大，但是它记录信息量大，且思维简单容易理解——不过它真正的致命缺点在于遇到负权边就会暴毙。
树形 DP
设 $d[x]$ 表示从 x 出发走向以 x 为根的子树所能够到达的最远节点的深度，$f[x]$ 表示经过 x 的树上最长链的长度，x 的子节点分别为 $y_1,y_2,…,y_k$，则可以得到 $d[x]=max_{1≤i≤k}(d[y_i]+edge[x,y_i])$。
对于 x 的任意两子节点 $y_i,y_j(j<i)$，我们可以将经过 x 的最长链长度拆成 4 个部分：$d[y_i],d[y_j],edge[x,y_i],edge[x,y_j]$。于是有 $f[x]=max_{1≤j≤i≤k}(d[y_i],d[y_j],edge[x,y_i],edge[x,y_j])$。
事实上我们没有必要使用 $y_i,y_j$ 两个参数来更新 $f[x]$—— 回顾一下 $d[x]$ 的定义：从 x 出发走向以 x 为根的子树所能达到的最远节点的深度 —— 在循环枚举到 $i$ 之前，$d[x]$ 所表示的就是 $max_{1≤j≤i}(d[y_j]+edge[x,y_j])$，当然这个值是 $f[x]$ 的一部分。也就是可以先用 $d[x]+d[y]+edge(x,y)$ 更新 $f[x]$，再用 $d[y]+edge[x,y]$ 更新 $d[x]$。
#define des edge[i].destinationVertex
inline void DP(int x){
vertex[x].vis = true;
for(int i=head[x];i;i=edge[i].nextEdge){
if(vertex[des].vis) continue;
DP(des);
treeLength = max(treeLength, vertex[x].depth + vertex[des].depth + edge[i].value);
vertex[x].depth = max(vertex[x].depth, vertex[des].depth + edge[i].value);
}
}
DP 方法的码量明显小于搜索方法，但是缺点也很明显，由于只关注状态的转移，DP 方法只能求出直径的长度，由于在树形图上搜索的时间复杂度也是 $O(n)$，DP 节约时间的方法在这里变成了它的劣势。但是 DP 方法也弥补了搜索方法最大的不足 —— 它可以处理负权边，可以说是一种短小精悍的方法了。
例题
一道我个人感觉挺好的题，这里当作例题来做：P3629 巡逻
题目大意
给定一棵 n 个节点的树，树上的每条边边权都为 1。我们规定“巡逻距离”是从 1 号点出发将树上所有遍历至少一次再回到起点所走过的边权和。现在在树上添加 1 或 2 条边，规定添加的边必须且只能走一次，求最短的巡逻距离。
思路
在还没有添加任何边的时候，巡逻距离显然是 $2*(n-1)$，因为在树上巡逻一次相当于做了一遍 DFS，每条边都会被递一次归一次 —— 换句话说，由于是一棵树，所以从 1 号点到达每一点的最短路径是唯一的，而对于每个节点 $vertex[i]$，直接连接它的边 $edge[j]$ 都会在到达 $vertex[i]$ 和从 $vertex[i]$ 返回时各被走一遍。
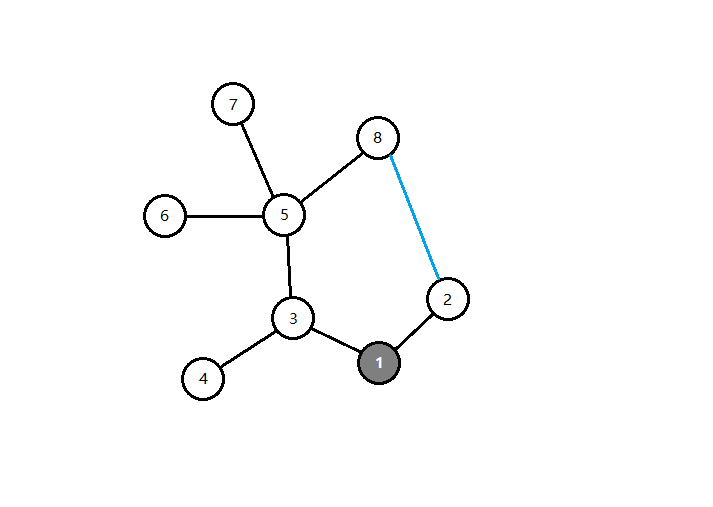添加一条边的时候也很简单，因为添加一条边相当于在图上添加了一个环，由于每条边都要巡逻到，我们要把这个环完整地走一遍。对于题目中给出的样例树，我们添加一条 $edge_{2,8}$，那么现在就有由 8，5，3，1，2 构成的环。原本遍历环上的边（除了新添加的那条）巡逻距离为 8，但是现在我们走这个环距离就只有 5 —— 环上每条边都少走了一次，取而代之的是走了一次新添加的边。对于树上的一条链，如果用其两端点为 $i,j$，其长度为 $chain[i][j]$，那么在这种情况下我们遍历这个链只需要 $chain[i][j]+1$ 的路程，即可以节约 $chain[i][j]-1$ 的路程。
所以添加一条边的时候，我们只需要求出树的直径长度 $treeLength$，巡逻路径长度便是 $2*(n-1)-(treeLength-1)$。
添加两条边时，我们按照上面的思路添加好第一条边，重点处理第二条边。添加第二条边就又增加了一个环，如果这个环与第一个环毫不相干，那么只需要按照上面的方法计算第二个环节约的路径长度。
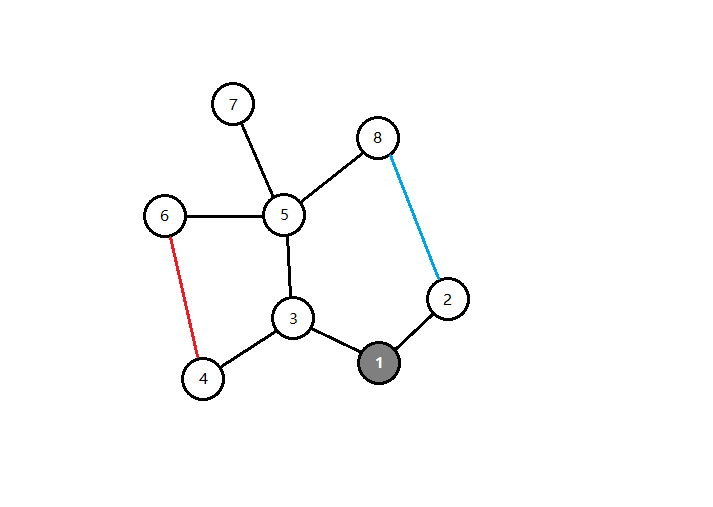但是当第二个环与第一个环有重合的边时，事情就没有那么简单了。对于题目中给出的样例树，再添加一条 $edge_{4,6}$，就形成了由 3，5，6，4 构成的第二个环。此时 $edge_{3,5}$ 既在第一个环上又在第二个环上。由于每条边都要被巡逻到，我们必须要把第二个环也完整地走一遍。这样一来 $edge_{3,5}$ 就被走了两边，和不添加任何边的时候相同。也就是说添加第一条边的时候减少的那次，又被走回来了。
我们可以认为添加一条边时求出的直径是“要被减少的距离”，因为有直径长度的边被少走了一次。现在添加第二条边时有些边少走的那一次被加回来了，我们可以将第一次求出的直径上的所有边权取负，这样在走第二个环的时候走上这些重合的边，将会在答案中减去这条边的边权，即“不仅没有再减少距离，反而还让本来被减少的边又被走了”。
再修改后的树上求直径添加第二条边，这个题就基本做完了。同添加第一条边一样，节省的路径长度是 $treeLength-1$。
回过头来看，第一次我们不仅需要求出树直径的长度，而且还需要求出直径的具体方案，因此使用两次搜索的方法；第二次只需要求出直径的长度，且因为修改后出现了负权边，所以要使用树形 DP 的方法求直径 —— 一次就把两种方法练了，这难道不是一道很妙的题吗？
Code
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<map>
#include<queue>
#define des edge[i].destinationVertex
using namespace std;
const int MaxN = 100005;
struct Edge{
int destinationVertex, nextEdge, value;
}edge[MaxN * 2];
struct Vertex{
int depth, father;
bool vis;
}vertex[MaxN];
int head[MaxN], tot, n, k, deepest, treeLength;
bool vis[MaxN];
inline void AddEdge(int u, int v){
tot++;
edge[tot].destinationVertex = v;
edge[tot].nextEdge = head[u];
edge[tot].value = 1;
head[u] = tot;
}
inline void Reset(){
for(int i=1;i<=n;i++){
vertex[i].depth = 0;
vertex[i].vis = false;
}
}
inline void BFS(int x, int secondTime){
Reset();
queue<int> q;
q.push(x);
vertex[x].vis = true;
while(!q.empty()){
int cur = q.front();
q.pop();
for(int i=head[cur];i;i=edge[i].nextEdge){
if(!vertex[des].vis){
vertex[des].vis = true;
vertex[des].depth = vertex[cur].depth + edge[i].value;
q.push(des);
if(secondTime) vertex[des].father = cur;
}
}
}
for(int i=1;i<=n;i++)
if(treeLength < vertex[i].depth){
treeLength = vertex[i].depth;
deepest = i;
}
}
inline void Change(int x){
while(vertex[x].father){
int fa = vertex[x].father;
for(int i=head[fa];i;i=edge[i].nextEdge){
if(des == x){
edge[i].value = -1;
break;
}
}
for(int i=head[x];i;i=edge[i].nextEdge){
if(des == fa){
edge[i].value = -1;
break;
}
}
x = fa;
}
}
inline void DP(int x){
vertex[x].vis = true;
for(int i=head[x];i;i=edge[i].nextEdge){
if(vertex[des].vis) continue;
DP(des);
treeLength = max(treeLength, vertex[x].depth + vertex[des].depth + edge[i].value);
vertex[x].depth = max(vertex[x].depth, vertex[des].depth + edge[i].value);
}
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<n;i++){
int u, v;
scanf("%d%d",&u,&v);
AddEdge(u,v), AddEdge(v,u);
}
if(k == 1){
BFS(1, 0);
BFS(deepest, 0);
printf("%d", 2 * n - vertex[deepest].depth - 1);
}
else{
BFS(1, 0);
BFS(deepest, 1);
int firstLength = vertex[deepest].depth;
Change(deepest);
Reset();
treeLength = 0;
DP(1);
printf("%d", 2 * n - treeLength - firstLength);
}
return 0;
}